1122
The value of x
(sh.itjust.works)
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
this post was submitted on 08 Oct 2024
1122 points (98.2% liked)
People Twitter
5403 readers
256 users here now
People tweeting stuff. We allow tweets from anyone.
RULES:
- Mark NSFW content.
- No doxxing people.
- Must be a pic of the tweet or similar. No direct links to the tweet.
- No bullying or international politcs
- Be excellent to each other.
- Provide an archived link to the tweet (or similar) being shown if it's a major figure or a politician.
founded 2 years ago
MODERATORS
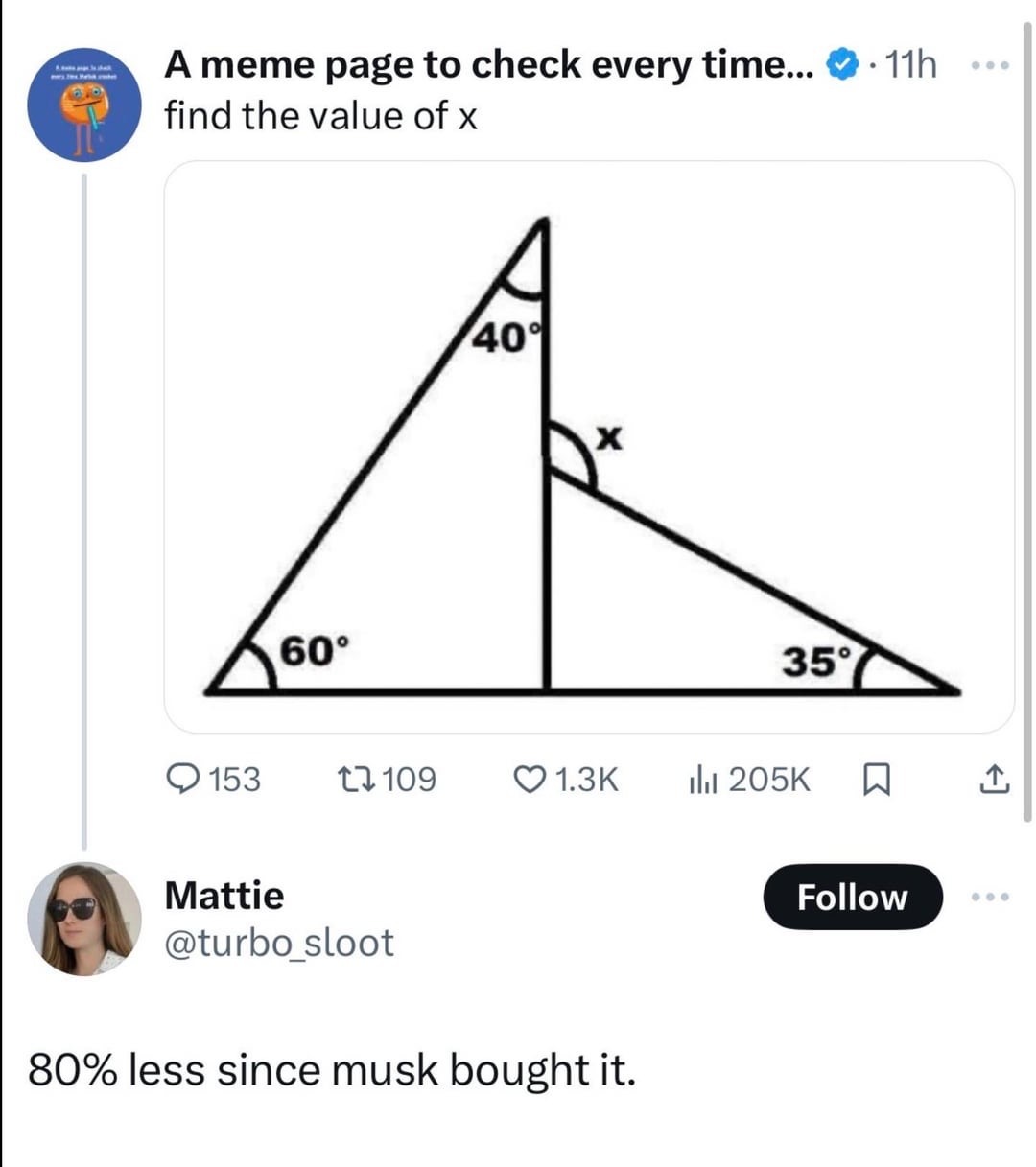
What a deviously misleading diagram.
The triangle on the left isn't actually a right angle triangle, as the other angles add to 100°, meaning the final one is actually 80°, not 90°.
Therefore the triangle on the right also isn't a right angle triangle. That corner is 100°.
100+35=135°. 180-135=45°. So that's 45° for the top angle.
X = the straight line of the joined triangles (180°) - the top angle of the right triangle (45°). 180-45=135°
X is 135°, not the 125° it initially appears to be.
It also doesn't say that the line on the bottom is straight, so we have no idea if that middle vertex adds up to 180 degrees. I would say it is unsolvable.
This is what I was thinking. The image is not to scale, so it is risky to say that the angles at the bottom center add up to 180, despite looking that way. If a presented angle does not represent the real angle, then presented straight lines might not represent real lines.
Eh, I think @sag pretty well nailed it.
Looks like an outer triangle with inner triangles so x = 180 - (180 - (40 + 60 + 35)) = 40 + 60 + 35 = 135
Can you clarify what you mean? this doesn't make sense to me. There isn't an "outer" triangle. There's one triangle (the left one) that has the angles 40, 60, 80. Both triangles are misleadingly drawn as they appear to be aligned at the bottom but they're not (left triangle's non-displayed angle is 80, not 90 degrees). So that means we can't figure out the angles of the right triangle since we only have information of 1 angle (the other can't be figured out since we can't assume its actually aligned at the bottom since the graph is now obviously not to scale).
I mean to me it looks like there are two connected triangles with an implied 3rd where x is the degree measure of its apex. IFF that is true, them you can assume 180 degree totals for each triangle individually and one for the "outer triangle".
I totally get it if you take the perspective that none of it is to scale, but it seems unreasonable to me that a straight line is not a straight line connecting the two triangles shown. Either it's unsolvable from that premise, or you can assume 3 triangles that compose one larger triangle and solve directly. And it seems weird to share something that is patently unsolvable.