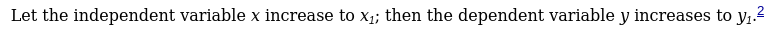This is a sequel to my previous post. The idea is the same, but I'm using better methods as was suggested in the comments.
As u/Sodium_nitride (thank you!) explained, here...
- ...I use a production matrix instead of the Cobb-Douglas function.
- ...I use capital-time instead of capital, to handle depreciation.
- ...classes consume commodities, seeking to maximize the amount consumed.
Also, I purchased the book suggested by u/davel :)
We use the following definitions:
- Labor is measured relative to A's total labor power.
- B has
blabor power, assumed to be proportional to population. - Capital-time and commodities are measured in units of what can be produced directly from 1 unit of labor.
- Labor sold is represented with
w, and the salary is used to purchase capital-times_kand commoditiess_c. - Consumption of A is
c, while that of B isz*b*c, wherezis the ratio of per capita consumption.
Production matrix:
/0 0 0\
A = |1 m 0|
\1 n 0/
Input vectors:
/ 1 - w \
x_A = |k_A + s_k|
\ 0 /
/ b + w \
x_B = |k_B - s_k|
\ 0 /
Demand vectors:
/ w - 1 \
y_A = | -s_k |
\c - s_c/
/ -b - w \
y_B = | s_k |
\z*b*c + s_c/
Payoff functions:
X_A = c
X_B = z*c
Case 1: full equilibrium
In this case, we assume that A and B can negotiate w, s_k and s_c freely,
with no party being able to obtain a better bargaining position.
The Nash equilibrium is:
w = s_k = s_c = 0
c = (m - n - 1)/(m - 1)
z = 1
That is, both groups are independent and produce their own capital-time and commodities. Their consumption is directly proportional to their labor power. Effectively, there is no difference between A and B, any member of either group belongs to the same class.
Case 2: asymmetric capital ownership
Here, we set k_A = s_k = 0, so A owns no capital-time. A and B can negotiate w and s_c
under the same conditions as in Case 1.
The Nash equilibrium is:
w = 1
s_c = c = (1/2)*(m - n - 1)/(m - 1)
z = 2 + 1/b
As can be seen, in this case A works for B and obtains a salary.
Interestingly, this salary is exactly half of what A would have obtained in Case 1. From this and z's non-dependence on
m and n, we can deduce that increases in productivity scale
both A's and B's earnings with the same coefficient, so it's impossible for B to force A's income to any specific minimum.
We also see that B's per capita income is higher when less people belong to the group. For a small enough group, B's total income approaches that of A, just extremely concentrated.
A plausible hypothesis here is that, if the initial situation is Case 2 but productivity is more than high enough to sustain A's needs (thanks to the inevitable scaling described before), then A would be able to eventually negotiate their way to the final equilibrium, Case 1, provided a minimally feasible way to obtain capital.
If that is the case, the (surreal, but theoretically interesting) requirements to get to the equilibrium could be summarized like this:
- All members of A cooperate perfectly (obviously false).
- B has no way to gain an advantage (bourgeois state in general).
- The productive forces have developed beyond a critical point.
Further questions
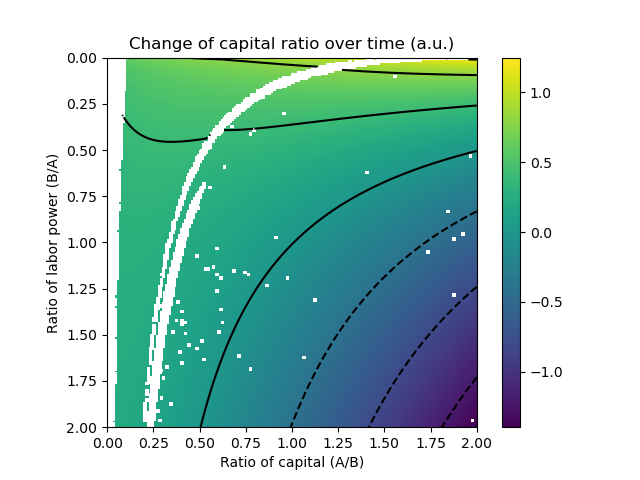
- How could one verify the hypothesis above? I know how to use production matrices in a state of equilibrium, but what about transient states?
- What if individuals can freely move across groups as their economic status changes and so do their interests? I know nothing about cooperative game theory, so this could be an interesting start.
- What if members of A and/or B do not cooperate perfectly?
- What are the minimum requirements for a mechanism that could allow the cooperative result in a non-cooperative Nash equilibrium?