1122
The value of x
(sh.itjust.works)
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
this post was submitted on 08 Oct 2024
1122 points (98.2% liked)
People Twitter
5377 readers
1095 users here now
People tweeting stuff. We allow tweets from anyone.
RULES:
- Mark NSFW content.
- No doxxing people.
- Must be a tweet or similar
- No bullying or international politcs
- Be excellent to each other.
- Provide an archived link to the tweet (or similar) being shown if it's a major figure or a politician.
founded 2 years ago
MODERATORS
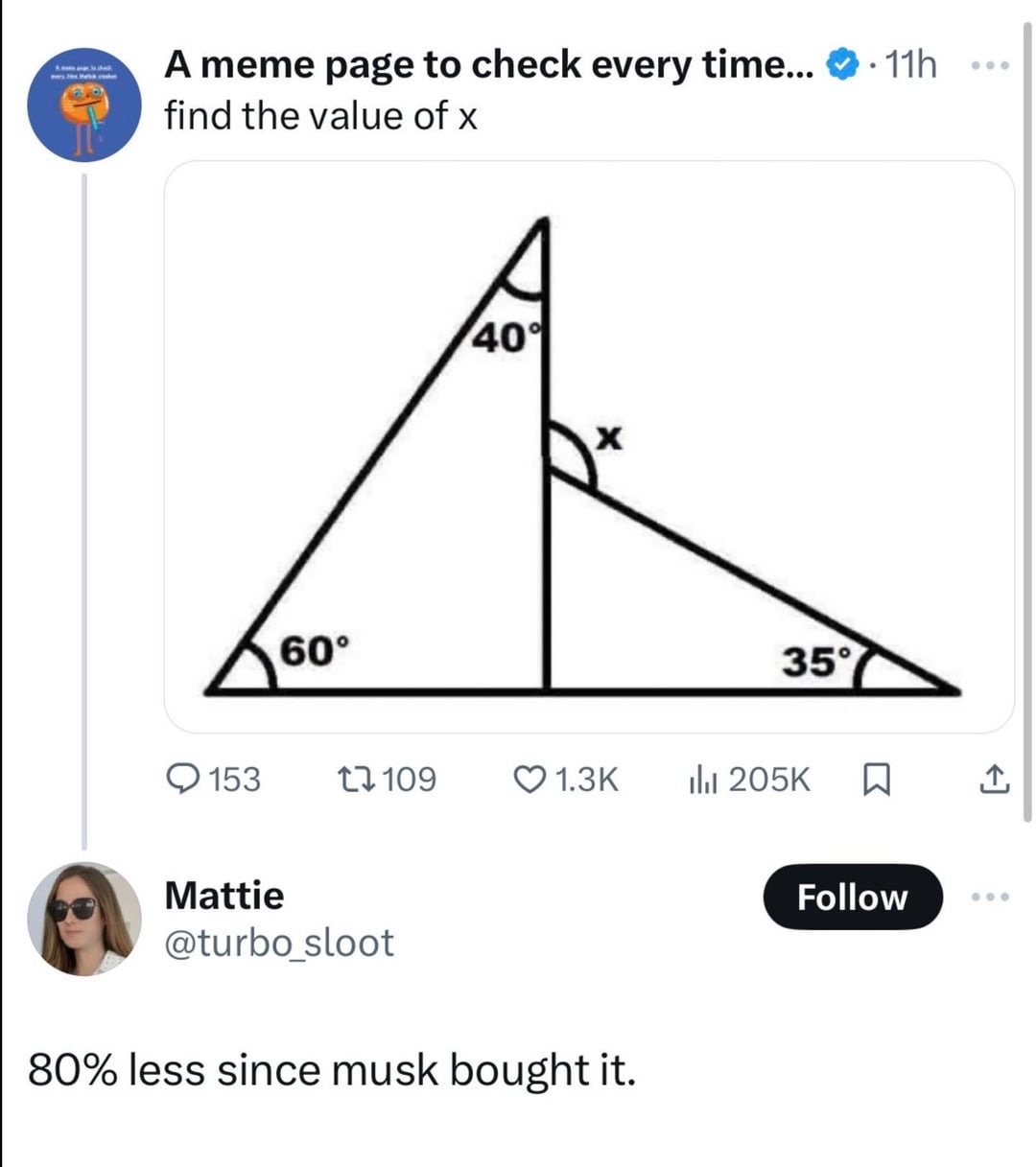
All these people saying its 135 are making big assumptions that I think is incorrect. There’s one triangle (the left one) that has the angles 40, 60, 80. The 80 degrees is calculated based on the other angles. What's very important is the fact that these triangles appear to have a shared 90 degree corner, but that is not the case based on what we just calculated. This means the image is not to scale and we must not make any visual assumptions. So that means we can’t figure out the angles of the right triangle since we only have information of 1 angle (the other can’t be figured out since we can’t assume its actually aligned at the bottom since the graph is now obviously not to scale).
Someone correct me if I'm wrong.
I mean, the assumption shouldn't be anything about scale. It should be that we're looking at straight lines. And if we can't assume that, then what are we even doing.
But, assuming straight lines, given straight lines you find the other side of an intersecting line because of complements.
We can't assume that the straight line across the bottom is a straight line because the angles in the drawing are not to scale. Who's to say that the "right angle" of the right side triangle isn't 144°?
If the scale is not consistent with euclidian planar geometry, one could argue that the scale is consistent within itself, thus the right triangle's "right angle" might also be 80°, which is not a supplement to the known 80° angle.