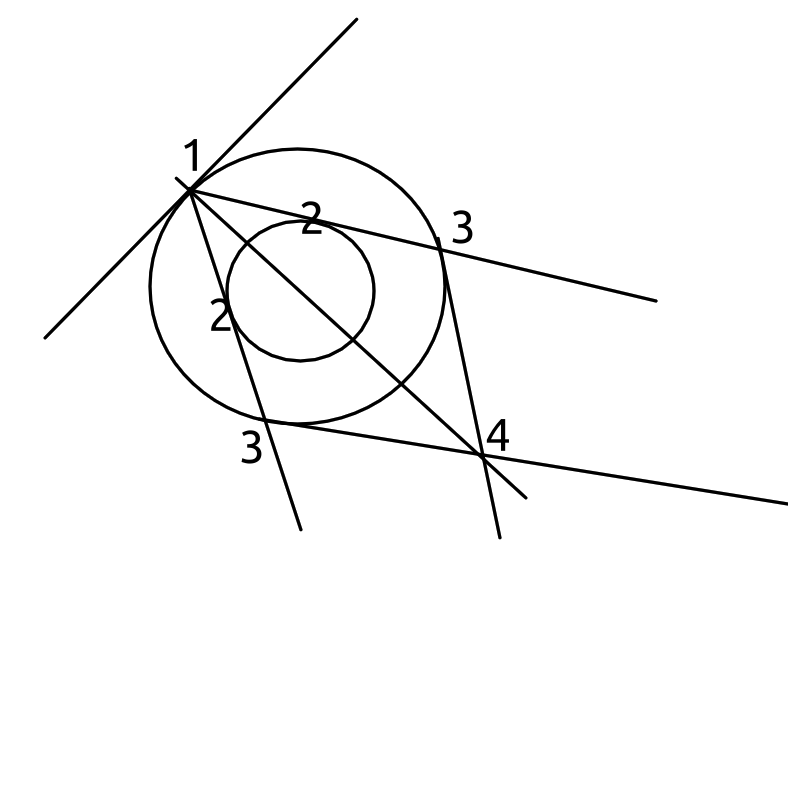
Here's a solution for circles with different radius that doesn't require right angle measurement or parallel lines:
- Draw a tangent on the larger circle
- Draw two tangents on the smaller circle that intersect where the first tangent touches the larger circle
- Draw two tangents on the larger circle where the tangents from step 2 intersect the larger circle opposite to the first tangent
- Find the intersection of the tangents from the 3rd step. A line from this to where the first tangent touches the larger circle must go through the center of the two circles.
- Repeat the above with the first tangent intersecting on a different point on the larger circle. The intersection of the lines from the 4th step is the center of the circle.
Edit: visual aid