Asklemmy
A loosely moderated place to ask open-ended questions
If your post meets the following criteria, it's welcome here!
- Open-ended question
- Not offensive: at this point, we do not have the bandwidth to moderate overtly political discussions. Assume best intent and be excellent to each other.
- Not regarding using or support for Lemmy: context, see the list of support communities and tools for finding communities below
- Not ad nauseam inducing: please make sure it is a question that would be new to most members
- An actual topic of discussion
Looking for support?
Looking for a community?
- Lemmyverse: community search
- sub.rehab: maps old subreddits to fediverse options, marks official as such
- !lemmy411@lemmy.ca: a community for finding communities
~Icon~ ~by~ ~@Double_A@discuss.tchncs.de~
For day-to-day purposes, if you are used to Fahrenheit but not Celsius or vice versa, and all you want to do is get a rough sense of how warm or cold it is outside without having to do arithmetic involving fractions in your head, then remember that there are two temperatures in Celsius that are roughly the same in Fahrenheit but with their digits transposed: 16° C ~ 61° F, and 28° C ~ 82° F. You can then roughly interpolate/extrapolate by about 2° F for every 1° C.
Also freezing is 0 in Celsius, so 32f is 0c. That one always helps me. Not as useful for converting c to f.
Do you remember the Fibonacci sequence? You can use it to convert miles to kilometers .
2 mi ~= 3km
5mi ~= 8km
8mi ~= 13km
13mi ~= 21km
And so on.
Wait, is this true until its not or is it true forever as you go higher in the sequence?
I think the way to formally prove this is to find the difference between the Fibonacci approximation and the usual conversion, and then to find whether that series is convergent or not. Someone who has taken the appropriate pre-calculus or calculus course could actually carry it out :P
However, I got curious about graphing it for distances "small enough" like from Earth to the sun (150 million km). Turns out, there's always an error, but the error doesn't seem to be growing. In other words, except for the first few terms, the Fibonacci approximation works!
This graph grabs each "Fibonacci mile" and converts it to kilometers either with the usual conversion or the Fibonacci-approximation conversion. I also plotted a straight line to see if the points deviated.
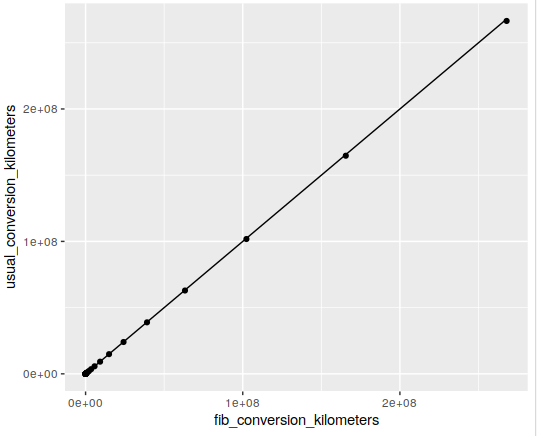
Edit: Here's another graph
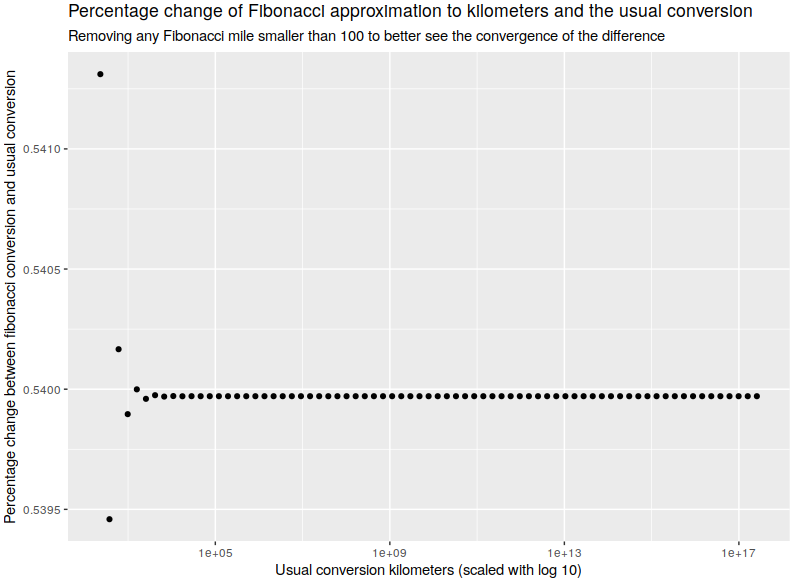
So it turns out:
- Fibonacci-approximated kilometers are always higher than the usual-conversion kilometers
- At most, the difference between both is 25%. That happens early on in the terms.
- After that, the percentage difference oscillates around a value and comes closer to it.
- When talking about more than 100 miles, the percentage change approximates 0.54.
TL;DR:
- Yes, the Fibonacci trick is true forever as you go higher in the sequence if you're willing to accept a 0.54% error.
If someone wants to play around with the code, here it is.
Note that you need RStudio and the Tidyverse package.
You just did the math!
The ratio of consecutive terms of the Fibonacci sequence is approximately the golden ratio phi = ~1.618. This approximation gets more accurate as the sequence advances. One mile is ~1.609km. So technically for large enough numbers of miles, you will be off by about half a percent.
It's true forever. The Fibonacci sequence used in this way converges on the golden ratio, which is close to the conversion of km and mi.
Someone already replied with a graph, but I also got curious and checked for some higher numbers. Sure enough, it held up.
For example:
832,040mi => 1,346,269km (actual: 1,339,039km)
The litany against fear

The mneumonic major system. Once I learned it by heart, it helped me memorize all kinds of numbers: cards, IDs, passwords, addresses…
That sounds a lot more complicated than just memorizing the number itself. How long did it take before you felt comfortable with this?
To give an extreme example:
"I solemnly swear that I am up to no good." vs. "053250411391271"
But to be fair, I never end up with nice sentences. It's more like "Thank you, rainbow. Clock firework" and I imagine myself thanking a rainbow and telling it to "clock firework", whatever that means…
As to how long, I think it could've been a couple of months doing a dozen or so conversions. In total it's a very small investment of time, assuming you space it out and don't cram. It really helps to use the Wikipedia mnemonics (like how 4 is kinda like a mirrored R).
Anyone who isn't at least mildly interested that you know Morse code isn't someone you want to know :-)
Good filter technique.
Simple recipe formulas that are scalable
Baker's ratios make my family think I'm a much better baker than I am.
Basic risen bread (a "60% hydration bread" ): 100 parts by weight of flour, 60-70 parts liquid, 3 parts salt, 2 parts yeast. Use grams and scale it up by 5 (500g flour), use water or beer for the liquid, knead, let rise for an hour or so, shape, rest for 30min, then bake at 400F for about an hour or until the inside is around 190-200F, and LET IT COOL to sub-120F before you cut in. Or if you're feeling fancy, use scalded and cooled milk, add 5-10 parts sugar, and swap out 10-20 parts of the liquid for melted but not hot butter - and you get a nice rich bread, half way to a brioche. Or go to 70-75 parts liquid, including some olive oil, and kneed for a long time, and you got a solid pizza dough.
Quick breads: 2 parts flour, 2 parts liquid (including sugar), 1 part beaten egg, 1 part fat (oil or melted butter). This gives you a jumping if point for banana breads, pancakes, muffins, and scones. Add or withhold a little liquid to get the consistency you want for how you're cooking it.
A crowd pleasing karaoke song!
I've never seen these flop at kareoke (if done with average competency):
Jump around - cypress hill gang
I will survive - Gloria Gaynor
Bohemian Rhapsody - Queen
Billy Jean - Michael Jackson (many other covers)
Shake it off - Taylor Swift
Pick 1 of the above plus a Beatles song and you're good for impromptu Kareoke.
If you have a few days notice and a friend to plan with the options expand...
I tried Bohemian Rhapsody once at karaoke, realized quick that I did not have the range for that song.
Learn some alphabets of foreign languages. Russian is fun because some of the characters looks like English letters but have completely different sounds. Korean is also cool because it looks crazy complex but it's actually extremely simple.
I don't know any Korean, but the Korean alphabet is by far the best writing system I've seen.
The characters make the shape your mouth makes while annunciating that letter. It's ingenious.
Subnets
/24 and /32 are like 90% of the battle. 256 hosts and 1 host solves most issues.
A completely random ordering of a deck of cards. You can have a deck pre-stacked in this order, learn some false shuffles, have someone pick a card and place it back anywhere they want without marking its location in any way, and when you inspect the deck you know exactly what their card is. And they'll never guess that the way you did it was memorizing the order of every card in the deck.
I'm sure there are a lot more advanced ways to take advantage of this, just a handy ability to have in your back pocket (literally).
If you're going to memorise a deck of cards, you're better off learning something like the Mnemonica Stack as you can use it as the basis for a whole load of card tricks.
How to pronounce names in different cultures.
Not necessarily the part for calculating the day of the week for any arbitrary day centuries ago, that's just a useless party trick, but for the current year so you don't need to pull out your phone to check. Knowing that 1/3 (or 1/4 on a leap year), the last day of February, 3/14, 4/4, 5/9, 6/6, 7/11, 8/8, 9/5, 10/10, 11/7, and 12/12 are all the same day of the week, that this year they're all Tuesdays, and next year they're all Thursdays, is mostly easy to remember and very frequently useful.
Thirty days has September, April, June, and November.
I always just used the knuckle trick for counting. The ones that have 31 days are at the top of the knuckle and the 30 (or 28/9) day months are in between the knuckles.
If you drive, the 3-4-8 second tailgating rule
Here is an alternative Piped link(s): https://piped.video/watch?v=QhGMm4aKWxc
Piped is a privacy-respecting open-source alternative frontend to YouTube.
I'm open-source, check me out at GitHub.
I have this thing about astronomy. Kind of a perspective thing of our place in the cosmos. I try to remember all the distances of planets from the sun and distances of moons from their planets. Also the diameters of solar objects. There's other factoids I try to remember about neighboring solar systems and galactic bodies. For example I remember the black hole at the center our galaxy is called Sagitarius A and its mass is 4M suns. The black hole at the center Andromeda our closest major galaxy at 2.5M light years is 25M suns. The black hole at the center M87, the closest active galaxy at 50M light years is 4B suns. I didn't look that stuff up so tell me if I didn't get it right.
Recipe for cooking. Useful for having a good meal and make other people love you.